
5.不确定性预算
0°/45°条件下SD BRDF绝对测量的相对不确定性预算
根据方程(15),在0°/45°条件下BRDF的相对不确定性可以表示为:
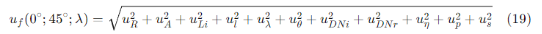
其中,uR和uA代表与测量几何因素相关的相对不确定性成分;uLi代表与光源稳定性相关的相对不确定性成分;UI、UDNi、μDNr、uη,代表与检测系统相关的相对不确定性成分,这些成分对应于入射和反射辐射检测的线性度和重复性以及放大因子的解算;uλ代表与波长相关的相对不确定性成分;uθ代表与入射角相关的相对不确定性成分;up代表与偏振相关的相对不确定性成分;us代表与杂散光相关的相对不确定性成分。
测量几何
因素使用1000毫米游标卡尺、百分表和连接杆测量距离R。使用内径尺测量开口面积A。R和A是通过多次测量的平均值获得的。测量精度为0.01毫米。测量过程如图17所示。距离和面积的测量不确定性通过多次测量的标准偏差描述。分别与R和A相关的相对不确定性成分如下:
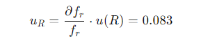


图17 (a)测量从积分球开口到样品表面的距离(b)测量光开口的面积
光源的稳定性
根据上文照明系统的描述,入射辐射的测量间隔不超过15分钟。根据图3,uLi≤0.015%。
线性度
线性不确定性可以表示为:
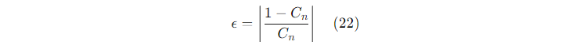
其中,Cn代表对应于非线性校正因子的第n阶数,∈代表非线性不确定性。
根据第3.4.2节的结果,可以计算出与硅探测器相关的相对不确定性成分为u(Si)=0.033%。根据FTIR光谱仪的工厂测试报告,光谱仪的线性度优于0.02%,即u(FTIR)=0.02%。
波长
根据PTFE的特性,SD的反射率在整个光谱范围内是平坦的(不包括2200nm附近的吸收带);因此,
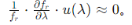
角度
根据图11,角度不确定性(0.1°)对0%/45°条件下的反射信号影响很小。因此,
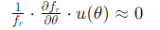
入射和反射信号检测的重复性
检测系统中的DN值是通过36次重复测量的平均值获得的。DN的n次重复测量的不确定性计算方法如下:
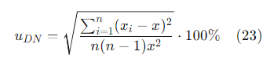
其中,xi代表第i次测量的DN值,x代表n次测量的平均值。与皮安表的DN相关的相对不确定性成分如表2-4所示,最大相对不确定性在波段范围内。
表2 探测器入射辐射的不确定性 (k = 1)
Incident Angle | Detector | ||||
Si | InGaAs | ||||
350–410 nm | 410–480 nm | 480–1000 nm | 1000–1600 nm | ||
0◦ | <0.01% | <0.01% | <0.01% | <0.01% | |
表3 探测器在 0° 反射处的 SD 反射辐射的不确定性 (k = 1)
Incident Zenith Angle | Detector | |||
Si | InGaAs | |||
350–410 nm | 410–480 nm | 480–1000 nm | 1000–1600 nm | |
0◦ | <0.01% | <0.01% | <0.01% | <0.01% |
15◦ | 0.10% | 0.03% | 0.01% | 0.04% |
30◦ | 0.12% | 0.04% | 0.02% | 0.05% |
45◦ | 0.16% | 0.05% | 0.02% | 0.05% |
60◦ | 0.22% | 0.07% | 0.02% | 0.06% |
75◦ | 0.31% | 0.15% | 0.04% | 0.16% |
表4 0° 入射时探测器的 SD 反射辐射的不确定性 (k = 1)
Incident Zenith Angle | Detector | ||||
Si | InGaAs | ||||
350–410 nm | 410–480 nm | 480–1000 nm | 1000–1600 nm | ||
15◦ | 0.10% | 0.02% | 0.01% | 0.02% | |
30◦ | 0.11% | 0.03% | 0.01% | 0.03% | |
45◦ | 0.11% | 0.03% | 0.01% | 0.03% | |
60◦ | 0.11% | 0.04% | 0.01% | 0.04% | |
75◦ | 0.12% | 0.04% | 0.01% | 0.04% | |
与 FTIR 光谱仪收集的 DN 数据相关的相对不确定度分量如图 18-20 所示。
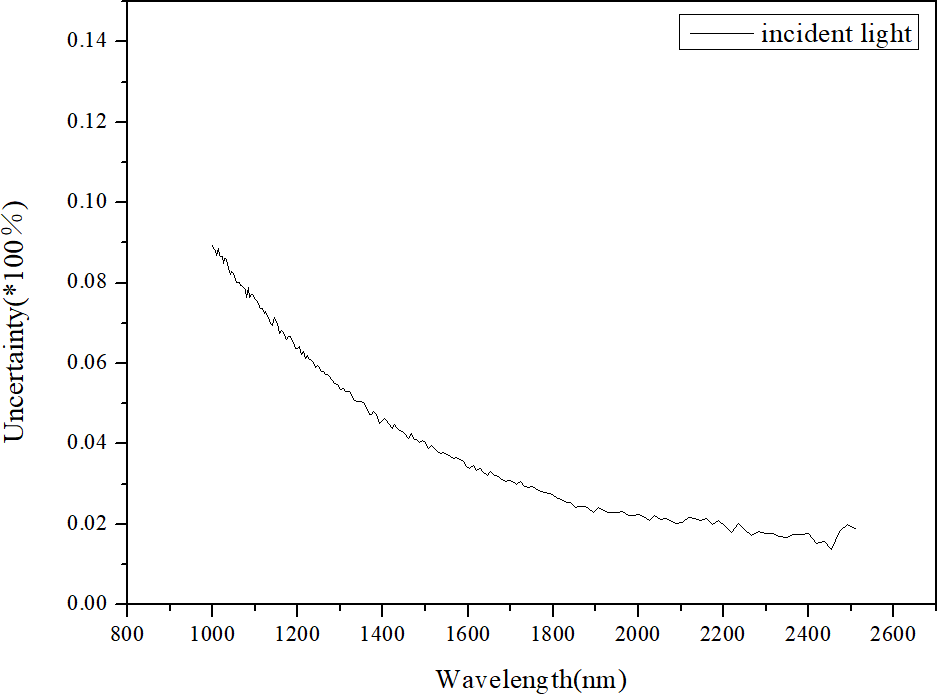
图18 FTIR 光谱仪的入射辐射的不确定度 (k = 1)

图19 FTIR 光谱仪在 0° 反射处反射辐射的不确定度 (k = 1)
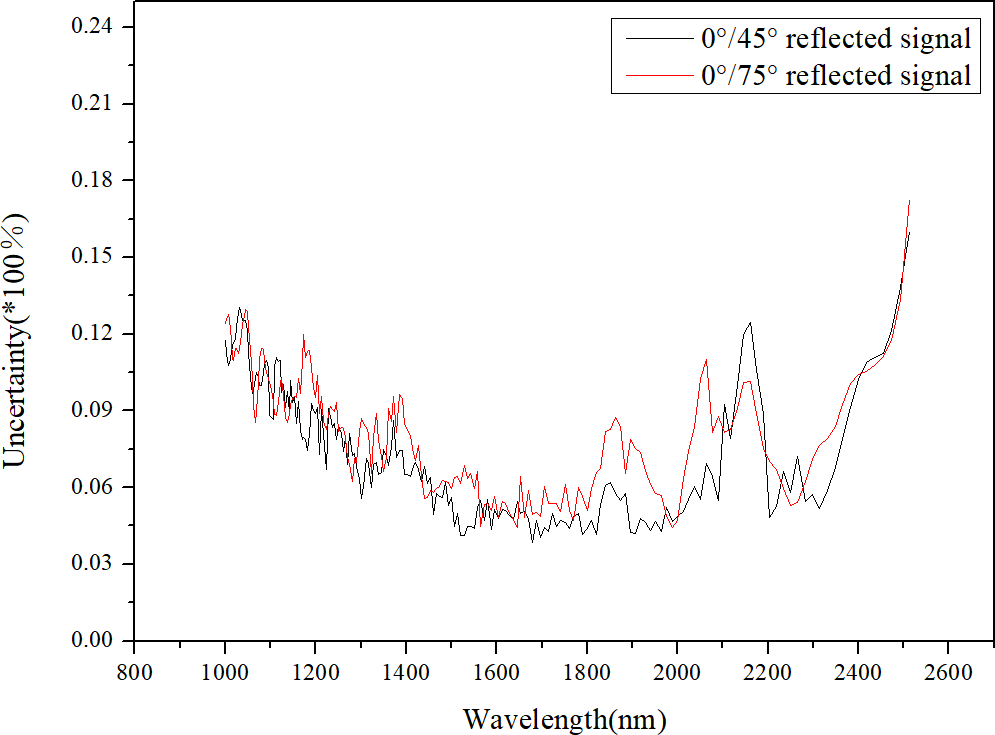
图20 FTIR 光谱仪在 0° 入射角处反射辐射的不确定度 (k = 1)
SD BRDF 在 0°/45° 的绝对测量的不确定度 (k = 2) 的计算结果如表5所示。
表5 在0°/45°条件下SD BRDF绝对测量的不确定性(k=2)
Component of Uncertainty | Type | Relative Uncertainty (%) |
Distance | A | 0.166% |
Aperture area | A | 0.096% |
Source stability | A | 0.03% |
Detector linearity Wavelength | B B | 0.066%(350–1000 nm) 0.04%(1000–2500 nm) <0.01% |
Rotation angle | B | <0.01% |
Incident radiation | A | <0.01% 0.22% (350–410 nm) |
Reflected radiation | A | 0.06% (410–480 nm) 0.02% (480–1000 nm) 0.24% (1000–2500 nm) 0.056% (1000–2500 nm) |
Scaling factor | B | |
Stray light | B | 0.2% |
Total | 0.36% (350-410 nm) 0.29%(410-480 nm)0.29% (480-1000 nm)0.37% (1000-2500 nm) | |
大角度下SD BRDF测量的相对不确定性预算
根据方程(18),大角度下SDBRDF测量的相对不确定性预算为:
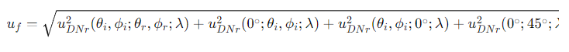
根据表2-4,不同反射角度下在0°入射角处的辐射相对不确定性与0°/45°处的辐射相对不确定性基本相同。在大入射角度下,不同反射角度下的辐射相对不确定性也与0°反射角度下的信号相同。即:
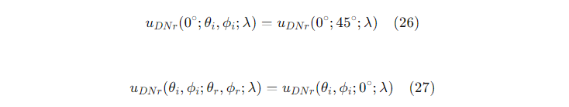
当u(θ)=0.1°时,0°入射角或0°反射角处反射辐射的相对不确定性(DNrθi,Φ;iθr,Φr;λ),DNr(θi,Φ;iθr,Φr;λ))较小,可以忽略。在大入射角和大反射角的极端情况下,相同角度不确定性下的反射辐射相对不确定性(DNr(θi,Φ;iθr,Φr;λ))小于0.15%。根据方程(25),基于互易定理的改进方法的不确定性如表6所示。
表6 使用改进方法测量 SD BRDF 的不确定度(k = 2)
Component of Uncertainty | Relative Uncertainty (k = 2) (×100%) | |||
350–410 nm | 410–480 nm | 480–1000 nm | 1000-2500nm | |
DNr(θi,ϕi;θr,ϕr;λ) | 0.62 | 0.30 | 0.08 | 0.45 |
DNr(θi,ϕi;0;λ) | 0.62 | 0.30 | 0.08 | 0.45 |
DNr(0°θi,ϕi;λ) | 0.22 | 0.06 | 0.02 | 0.24 |
DNr(0°;45°;λ) | 0.22 | 0.06 | 0.02 | 0.24 |
f(0°;45°;λ) | 0.36 | 0.29 | 0.29 | 0.37 |
θi | 0.30 | 0.30 | 0.30 | 0.30 |
Total | 1.04 | 0.60 | 0.43 | 0.86 |
改进方法与绝对测量方法在大角度下的测量不确定性比较
图21显示了使用第2节和第4.2节中两种方法测量大入射角(75°)时SDBRDF的不确定性。绝对测量方法的不确定性预算与第5.1节中给出的类似。不同之处仅在于第5.1.5节。在75°入射角(入射天顶角为75°)下的SD的绝对BRDF测量为:

图21两种方法在75°入射角下的不确定性(k=2)。可以根据方程(20)获得绝对BRDF测量方法的不确定性。在410nm到1000nm范围内,基于互易定理的改进方法将测量不确定性降低了50%以上。由于比较测量减少了测量不确定性对测角仪系统角度精度的依赖,测量精度显著提高。然而,在350nm到410nm和1000nm到2500nm范围内,测量精度的改普有限。这是因为在这些波段内,反射辐射的信噪比(SNR)较低。
6.结果
在0°/45°条件下的SD BRDF测量范围为350 nm至2400 nm。结果如图22所示.

图22 0°/45° 处的 SD BRDF
图 22 显示了在 0° 预估和 45° 反射条件下的 SD BRDF。
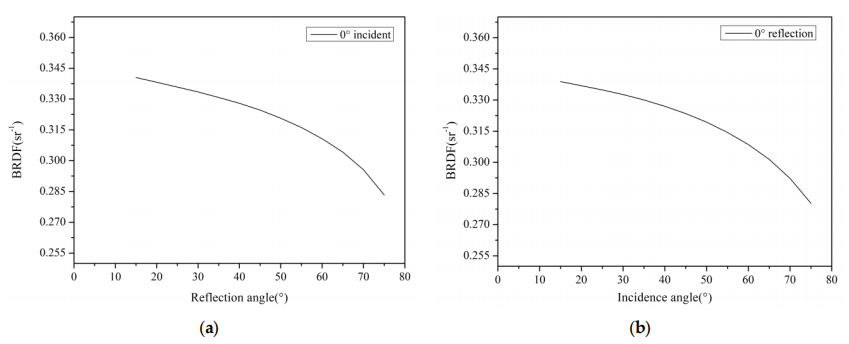
图23 (a)在0°入射条件下,不同反射角的SD BRDF。(b)在0°反射条件下,不同入射角的SD BRDF。
在将入射角或反射角固定为0°时,测量了650 nm处的SD BRDF,结果如图23所示。
使用基于互易定理的改进数据处理方法获得的一些SD BRDF测量结果如图24所示。入射和反射角度来自HY-1C卫星上的在轨校准系统。

图24 565 nm处反射天顶角为41.4°、方位角为117°时不同入射方位角和入射天顶角的SD BRDF
7.结论
在轨校准中,由于受到卫星轨道、在轨校准时间及其他因素的限制,不可避免地需要测量SD BRDF在平面内外和大角度几何条件下的值。本文提出了一种基于互易定理的改进数据处理方法,以实现太阳反射波段中SD BRDF在平面内外和大角度几何条件下的在轨校准。结果表明,在350 nm至410 nm范围内,测量不确定性(k=2)优于1.04%,在410 nm至480 nm范围内优于0.60%,在480 nm至1000 nm范围内优于0.43%,在1000 nm至2400 nm范围内优于0.86%。
与绝对测量方法相比,在410 nm至1000 nm范围内,改进方法的测量精度显著提高,测量不确定性减少了一半。在紫外和近红外波段中,改进的测量方法的提升有限,因为该方法将绝对测量方法中不确定性的角度依赖性转移到了辐射检测的准确性上。这也是紫外和近红外波段测量中不确定性较高的原因。不同的灯泡可以用来改善入射辐射。我们计划在未来的工作中探索通过改进反射辐射的测量精度来提高测量精度。