
用于太阳能反射波段的机载校准的高精度太阳能漫射器BRDF测量
1.引言
在太阳反射波段,基于太阳漫射体(SD)的在轨校准方法可以实现光学遥感器的全孔径、全视场和端到端的绝对辐射校准。SD的双向反射分布函数(BRDF)是影响在轨校准精度的关键参数。在发射前,需要在实验室中对SD BRDF进行高精度测量。由于测角仪系统的不确定性、偏振效应以及其他因素,在大入射角下,SD BRDF的测量不确定性远高于在0°入射天顶角和45°反射天顶角下的测量不确定性。本文报道了一种绝对BRDF测量装置。该测角系统由高亮度积分球作为辐射源、六轴机器人手臂和大型旋转台组成。测量波长范围从350 nm到2400 nm。
光学遥感器需要进行绝对辐射校准以量化传感器对已知辐射输入的响应。尽管遥感器在发射前已经进行了高精度校准,但在运输、发射和在轨操作过程中,其性能不可避免地会发生变化。因此,需要进行在轨校准。在各种在轨校准方法中,基于太阳漫射体(SD)的在轨校准方法具有高频率、全孔径、全视场和端到端的特点。这是当前太阳反射波段中主流的在轨校准方法。在这种校准方法中,利用SD反射的太阳辐射作为高辐射源。当传感器孔径在观测SD时,其辐射亮度直接受到SD BRDF的影响。因此,SD BRDF是决定在轨校准不确定性的关键参数。
BRDF能够准确描述物体的空间和光谱特性。它定义为从给定方向照射到物体表面的辐照度与其在另一方向反射的辐射亮度之比。用于在轨校准的初始SD BRDF只能在发射前的实验室中测量。进入轨道后,可以通过SD稳定性监测器或备用SD来监测BRDF的稳定性。
2.绝对BRDF测量原理
BRDF 可以定义为:
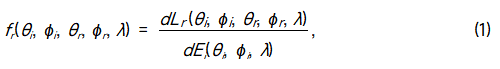
其中,dLr,表示由无限小元素在给定方向上反射的辐亮度;dEi表示从入射方向落在此无限小表面上的辐照度;θi和φi;分别表示入射方向的天顶角和方位角;θr和φr,分别表示反射方向的天顶角和方位角;λ代表波长。Θi,φi,θr,φr的几何关系如图1所示。

图1 入射光束和反射光束的几何关系
根据辐亮度和辐照度的定义:

其中,dE⟂(λ)和dE⟂(λ)分别表示当入射方向垂直于样品时的辐照度和辐亮度,Ω代表照明立体角。
方程(2)可以代入方程(1),同时对两边积分:

这些测量可以在狭窄的立体角和小表面上进行;辐射源的输出在空间方向上是均匀的。用于机载校准 的SD是一个几乎完美的漫射器。因此,f(θi,φi;θr,φr;λ)和L⟂(λ)可以认为是常数。
然后:

其中,R表示从辐射源开口到样品中心的距离,A表示辐射源开口的面积。方程(4)表明,通过测量入射辐亮度、照明立体角和反射辐亮度,可以获得所需的SD BRDF。
入射辐亮度和反射辐亮度使用相同的检测系统进行测量,最终的BRDF计算仅需要入射辐亮度与反射辐亮度的比率;因此,不必知道测量的辐亮度的绝对值。因此,方程(4)可以表示为:

其中,DN(θi,φi;θy,φr;λ)和DN⟂(λ)分别表示探测器测得的反射和入射辐亮度的数字量(DN)。为简化表达式,本文中从DN中减去了暗电流。
3.设施描述与校准
一个绝对BRDF测量装置如图2所示。它由三部分组成:一个辐照系统、一个测角仪系统和一个检测系统。所有设备都连接到同一台工业控制计算机。样品的BRDF可以通过控制软件自动测量。

图2 绝对BRDF测量装置
照明系统
选择积分球作为辐射源,以确保满足照明系统的亮度和均匀性要求,并减少偏振对测量结果的影响。

图3 一体化球形散热器
图3展示了球体辐射器的内涂层。涂层由压制的PTFE制成,反射率超过99%。球体的内径为150 mm,内置三个400 W的卤素灯。球体配备了水冷和空气冷却系统。当球体辐射器工作时,电源设定为1000 W(约为额定功率的80%)。在球体辐射器出口前加装了杂散光罩,以减少测量过程中杂散光的影响。
为了验证球体辐射器的均匀性,搭建了一个专门的均匀性测量设施。选择1:1成像比例的成像光学系统,并将其安装在二维XY平移台上。步进间隔设定为2 mm,扫描区域覆盖球体辐射器的整个开口。结果显示,开口的非均匀性小于0.5%。

图4球形散热器稳定性试验结果
球体辐射器的稳定性可以通过设施的检测系统来监测。设施调整到测量入射辐射的位置,将高精度电流源的输出功率设定为1000 W,测量波长为350 nm。经过30分钟的预热后,测量持续80分钟,采样间隔为20 ms。结果如图4所示。稳定性以相对标准偏差表示,光源的不稳定性在80分钟内小于0.06%
测角仪系统
测角仪系统的六轴机器人手臂和大型旋转台如图5所示。机器人手臂用于三维旋转样品,旋转台用于一维旋转照明系统。检测系统固定,以确保高精度辐射测量。

图5 测角仪系统
该设施的 BRDF 测量角度范围如表 1 所示。
表1 BRDF 测量的角度范围
角度参数 | 范围 (° ) | 备注 |
入射天顶角 (θi ) | 0–75 | 由于辐射源的遮挡,入射光线与反射光线之间的角度大于10◦ |
入射方位角 (ϕi ) | 0–360 | |
反射天顶角 (θr ) | 0–75 | |
反射方位角 (ϕr ) | 0–360 |
在SD表面定义了两个坐标系:机器人工具坐标系XYZ和BRDF坐标系xyZ。它们共享一个公共坐标原点,该原点位于样品的中心。这一点也是旋转阶段期间旋转轴与球形辐射源开口中心线的交点。图5显示了两个坐标系统的相对位置。机器人手臂绕机器人工具坐标系XYZ轴的旋转角度可以定义为ɑ、β、γ、δ而旋转阶段的旋转角度为δ。根据在两个坐标系中,入射矢量、反射矢量和样品法线之间的不同表达关系,θi、Φi、θr、Φr与α、β、γ、δ之间的关系可以建立如下:

对于给定的BRDF角度(θi、Φi、θr、Φr),机器人手臂和旋转阶段的旋转角度(ɑ、β、γ、δ)可以通过方程(6)-(9)计算出来。然后,根据计算出的ɑ、β、γ、δ旋转测角仪系统,以实现测量所需的几何关系。
检测系统
SD可以将入射辐射反射到半球体中,因此在测量过程中只有一小部分入射辐射被收集。设施的检测立体角非常小,约为0.003 sr,根据辐射源的不同入射角,入射辐射和反射辐射之间的差异约为四个数量级。对于不同的测量波长,这一差异甚至可能超过四个数量级。在如此大的动态范围内,需要确定并校正检测系统的非线性。
检测系统有两种配置。一种是单色仪、探测器和皮安计的组合;另一种是傅里叶变换红外(FTIR)光谱仪。这两种检测装置共享相同的前端光路系统。根据所需波长,使用平面反射镜和电动平移平台的组合来切换光路。
前端光路如图6所示。它由五个平面镜、三个凹面镜和一个电动平移平台组成。来自样品的反射辐射经过平面镜1和平面镜2反射后与光路平台平行,然后经过凹面镜1汇聚。然后,光线被平面镜3反射到光路切换装置,该装置由电动平移平台和平面镜组成。通过光路切换装置后,凹面镜将光线汇聚到单色仪或FTIR光谱仪的光学入口。
电动平移平台控制平面镜的前后移动。如图2所示,当平面镜位于光路切换装置的红色虚线框位置时,它将辐射反射到FTIR光谱仪的光学入口。而当其完全移开(位于黄色虚线框位置)时,辐射进入单色仪的光学入口。

图6 检测系统的光路图
电动平移平台控制平面镜的前后移动。根据图2,当平面镜位于光路切换装置上的红色虚线框位置时,它将辐射反射到FTIR光谱仪的光学入口。此外,当平面镜完全移除(位于黄色虚线框位置)时,辐射进入单色仪的光学入口。
在这两种配置下,检测设备的性能如下:
单色仪、探测器和皮安表:单色仪在350nm到600nm波长范围内的光谱分辨率约为3nm,在600nm到1700nm波长范围内的光谱分辨率约为6nm。根据不同的测量波长,配备了两种类型的探测器:硅探测器(350nm到1000nm)和lnGaAs探测器(1000nm到1700nm,双级TE制冷,-40°C)。所有光电信号由皮安表检测,测量结果传输到计算机进行数据存储和计算。
FTIR光谱仪:在测量设施中,选择InGaAs探测器作为VERTEX80的探测器。测量的光谱范围设置在11764cm-1(850nm)到4148cm-1(2410nm),光谱分辨率设置为64cm1(4.6nm到36.6nm)。选择此分辨率是因为SD反射率的光谱特性(光谱平坦性)以及在测量反射辐射时信噪比(SNR)的提高。在反傅里叶变换过程中,使用BlackmanHarris 4-Term作为加窗函数;零填充因子为2;选择功率谱模式进行相位校正;并选择绝对最大值作为峰值位置检索模式。
在测量反射辐射时,FTIR光谱仪使用的电路放大系数与用于入射辐射的系数不同,以确保足够高的信噪比。缩放因子η的计算方法如下:

其中,DNrFTIR(0°;45°;λ)和DNrFTIRX)分别表示FTIR光谱仪在0%45°反射辐射和入射辐射时的数字量(DN),而DNrInGaAs(0°;45°;λ)和 DNiInGaAs(X)分别表示InGaAs探测器在0°/45°反射辐射和入射辐射时的数字量(DN)。
将InGaAs探测器在0/45°条件下的入射辐射和反射辐射的DN比值与FTIR光谱仪在相同条件下的DN比值进行比较。选择1200nm和1300nm波段的数据进行计算。平均缩放因子为99.10。
系统校准
几何校准
设施的几何校准分为两个主要方面:确定BRDF测量的初始位置(机器人手臂的旋转中心和旋转台的原点)并验证旋转角度的不确定性。
机器人手臂的旋转中心位于旋转台的旋转轴与球体辐射器开口中心线的法线的交点处。测量前,需要确定样品的初始位置。

图7 (a) 测量光束的原理 (b) 通过测量光束确定旋转轴的原理
使用从球体辐射器开口发出的激光束作为指示器,并使用机器人手臂作为测量工具(测量原理如图7a所示),通过测量在不同角度下从球体辐射器开口发出的激光束(测量示意图如图7b所示)获得旋转台的空间线性方程,并初步建立机器人的基座坐标系与实验室坐标系之间的转换关系。然后,将激光束调整为垂直于旋转台的旋转轴,并根据入射激光束在工具坐标系Y轴上的位置和轴线方程确定实验室坐标原点的位置和两个坐标系的变换关系。建立仪器的校准模型,计算旋转中心在空间中的位置和姿态,并确定样品的初始位置。这种校准方法在文献中有详细描述。

图8 (a) 逆时针旋转辐射源并收集反射辐射 (b) 顺时针旋转辐射源并收集反射辐射。
如果逆时针旋转的角度是θal,θa2,···,θa10,顺时针旋转的角度是θb1,θb2,···,θb10,且校正前的原点角度为△θ,则

旋转阶段原点的校正值可以使用方程(11)计算。校正后,反射辐射如图9所示。DN(θai)和DN(θbi)的相对偏差小于0.2%:


图9 校正后在不同入射角下的反射辐射
采用基于镜面反射原理的检测方法来验证测角仪系统的角度不确定性。将坐标纸的原点放置在入射光束中心点处,前提是辐射源逆时针旋转180°后。假设辐射源的逆时针旋转角度为△δ,然后调整机器A,1使反射器绕Y轴旋转△δ/2,并记录此时反射光束中心点的位置。实验示意图如图10所示。

图10 (a) 确定坐标纸的原点 (b) 镜面反射测试
Δδ 的范围设置为6°到75°,并每隔3°进行一次测量。坐标纸与旋转中心之间的距离为1900毫米。实验结果如图11所示,在每个点旁边标记了测量点时的入射角。

图11 基于镜面反射的反射光斑位置数据测量(每个点旁边标记了入射角)
角度误差△θ可以表示为:

其中,xm和ym分别表示当前角度下反射光斑在坐标纸上的水平和垂直坐标;l表示坐标纸与旋转中心之间的距离。根据图11并使用方程(12)计算结果,最大偏差角为0.0769°,这意味着测角仪系统的角度精度小于0.1°。
检测系统的非线性校准

图12 探测器非线性测量结果
350 nm到1000 nm:采用基于积分球内两个发光二极管(LED)通量叠加的方法来检测探测器系统的非线性。测量范围为12 pA到364 nA,匹配了设施的动态范围。测量结果如图12所示。
1000 nm到2400 nm:FTIR光谱仪的线性不确定性由制造商测量,值为0.02%
设施的绝对测量工作流程
设施的测量步骤如下所示。首先,机器人夹持样品并将其移至避让位置,然后将辐射源从旋转台原点逆时针旋转180°。测量所需波长下的入射辐射。然后,软件控制辐射源和样品移动到所需测量位置,并测量样品的反射辐射。在反射辐射测量完成后,设施返回并再次测量入射辐射。软件可以通过设置反射辐射采集的数量来控制入射辐射的采集频率。通常,将反射辐射的采集次数设为10次,以确保入射辐射测量间隔不超过15分钟。测量过程的照片如图13a和13b所示。

图13 (a) 辐射源辐射的测量 (b) 样品反射辐射的测量。
4.用于在轨校准的SD BRDF测量
SD BRDF测量角度的确定
在轨校准通常在卫星点亮后和卫星次点亮前进行(图14)。基于对国际卫星上高光谱仪器观测结果的分析,在轨校准容易受到来自地球和大气层的散射和反射杂散光的影响。选择适当的太阳-地球-卫星(SES)角度来进行在轨校准时间,以减少这种影响。例如,在温室气体观测卫星(GOSAT)上的在轨校准SES角度刚好高于105°[28]。
在确定卫星校准时间和卫星轨道参数后,也就确定了入射光束的仰角和方位角。根据基于SD的在轨校准设施的设计要求,还可以确定校准时间时有效载荷中心轴(观测方向)的方向。
SD的姿态由入射方向和观测方向的矢量决定。要求入射方向和观测方向的天顶角尽可能小,并避免入射方位角和观测方位角的镜像位置。
然而,如果入射矢量和观测矢量之间的角度较大,无论SD如何放置,都无法减小入射方向和观测方向的天顶角。如果观测方向的天顶角过大,为了确保探测器的整个视场都被覆盖,SD的光学表面的尺寸将会增加。过大的SD会占用大量空间,影响卫星中其他系统的设计。因此,通常会设计一个较大的观测天顶角和较小的反射天顶角.

图14 在轨校准时间的示意图
基于互易定理的改进数据处理方法用于测量大角度BRDF
根据方程(5),绝对BRDF测量的不确定性可能与入射角的不确定性有关,且与入射角相关的相对不确定性成分uθi,为:

对于压制的PTFE,角度对DNr(θi,Φi;θr,θr;λ)的影响较小。在入射角和反射角较大的极端情况下,与角度相关的反射辐射分量的相对不确定性在u(θ)=0.1°时小于0.15%。在大入射角下,角度不确定性对DNr(θi,Φi;θr,θr;λ)的影响远小于对cosθi的影响。因此,设计了一种基于互易定理的改进数据处理方法,用于测量大角度BRDF。该方法的原理是,以垂直检测为参考,通过比较倾斜观测和垂直观测的BRDF来获得倾斜观测的BRDF。
根据方程(5),绝对BRDF测量的不确定性可能与入射角的不确定性有关,且与入射角相关的相对不确定性成分uθi,为:


对于压制的PTFE,角度对DNr(θi,Φi;θr,θr;λ)的影响较小。在入射角和反射角较大的极端情况下,与角度相关的反射辐射分量的相对不确定性在u(θ)=0.1°时小于0.15%。在大入射角下,角度不确定性对DNr(θi,Φi;θr,θr;λ)的影响远小于对cosθi的影响。因此,设计了一种基于互易定理的改进数据处理方法,用于测量大角度BRDF。该方法的原理是,以垂直检测为参考,通过比较倾斜观测和垂直观测的BRDF来获得倾斜观测的BRDF。

图15 与入射角相关的相对不确定性成分
互易定理描述了光路的可逆性。它指的是在表面或被动介质上进行任意反射或折射后,光束发射的能量与光束沿相反路径发射的能量相等。当应用于BRDF时,当入射角和反射角互换时,BRDF保持不变:

与倾斜照明(θ≠0°)相比,垂直照明(0;=0°)时,方程(12)中θi的影响最小。因此,使用在0°45°条件下测量的BRDF作为参考,来获得相同辐照度下其他角度的BRDF。然后,


其中DNi代表入射辐亮度的DNi值。根据方程(14),

对于其他非垂直辐照条件,

改进的数据处理方法的测量过程如图16所示。

图16 改进的数据处理方法的测量过程